Problem statement
King Arthur had the knights play a game, first he put numbers on the chairs beginning 1 and continuing around thi table, with one chair for each knight. Every chair was occupied, and King Arthur remained standing. He stood behing chair 1 and said, "You're In." Next he moved to the knight on chair 2 and said, "You're Out," and the knight left his seat and went off to stand on the side and watch the rest of the game. He then said to chair 3, "You're In." This pattern continued around the table till there was one winning knight who stayed seated.
If you knew how many knights were going to be at the table, how could you quickly determine which chair to sit so that you would win?
If you knew how many knights were going to be at the table, how could you quickly determine which chair to sit so that you would win?
Process
|
When we were first introduced to this problem, we were told to reflect for 5 minutes questions or ideas we could do to start this problem. As a group we shared our ideas and agreed on drawing it out to visualize it, and finding a pattern based on making a table; k for knights, and w for the winning chair.
We realized that the winning chair was 1 by each power of 2, so we knew the equation we were suppose to come up with had to have something to do with this rule. After a while of being stuck, we asked our teacher to help us out a bit because we were having problems with writing an equation for it. Time ran out and we didn't get to solve this on our own, and a group who came up with one shared and explained to the class. The next day we tested out this problem in real life. Both classes got there chairs and took them down to the field and we set up in a circle. Since we knew the equation many students were trying to sit in the correct spot to win by doing the math with the equation. |
Solution
|
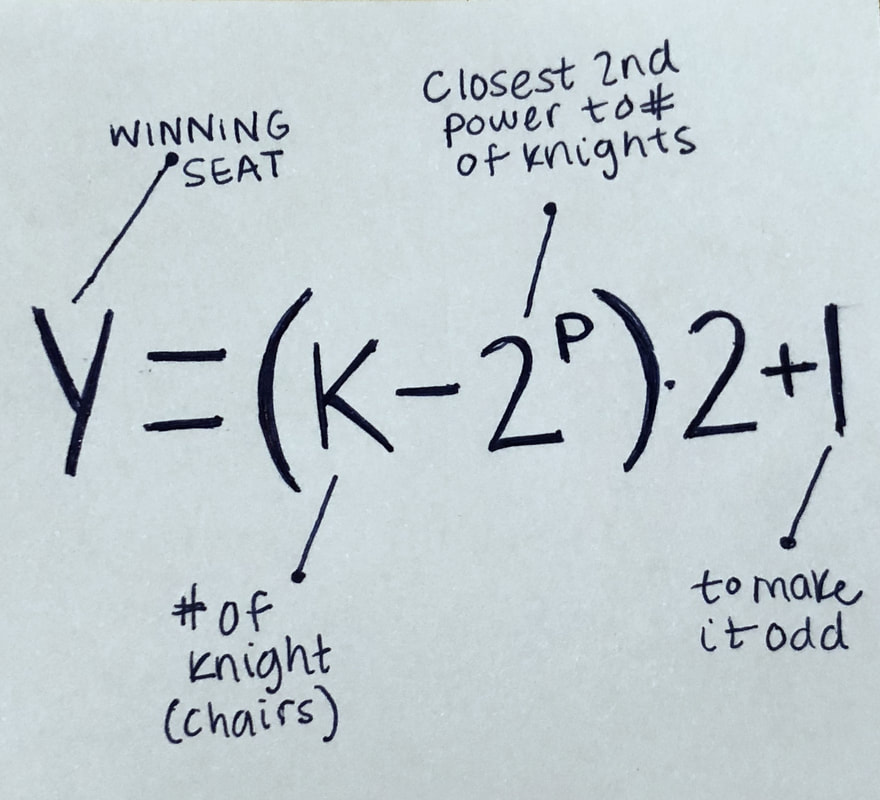
The solution is subtracting the number knights by the nearest creates integer of base 2 exponent. After that multiply by 2 and add 1 for the winning seat.
Another group shared their equation with the class that can find the winning seat for as many knights. Y=(K-2^P)2+1 K, represents the number of knights/chairs in the table. P, being the power of 2; closest to the power of k. This works because it would give us the right answers for odds or evens. We didn't have to do the steps of having to write them out and crossing them one by one. |
evolution/reflection
Something that pushes my thinking is having those 5 minutes to think about the problem by myself. Sometimes it's difficult seeing things on your own without a little help. I think my group did a really good job communicating because when we found something new we would share our ideas and make steps for what we should do next. Although this was a little challenging for me because I wanted to keep trying to solve for the problem because this might've slowed us down a bit, we were all at the same page which was good. Although we didn't come up with an equation to solve, we did end up understanding what was actually happening in the problem. I think it was super clear when recognizing when we needed help because we completely blanked out and didn't know what to do. Something my group did well too was asking for the help because any of us were confident enough to take the initiative to ask questions to our group peers or the teacher. This was easy for us because we wanted to solve the problem, it felt like a necessity and the only way to move forward was asking for some help. I think I was able to help peers because most of the time I understood what we were doing, and if someone didn't I was helped by explaining to them because I understood it. In the first initial stages of the problem my group was great at putting out ideas, right or wrong. We started throwing them out so we could constantly be moving our pencils and see what does or doesn't work. I think the group quiz helped to understand the first problem a lot better, it clarified the question I had about the first one. It made sense in the same way but the opposite since I the quiz we had the same problem but tweaked a bit. I would give myself an A on the problem because we had very good communication and our papers were full of notes since we were trying so many things together.