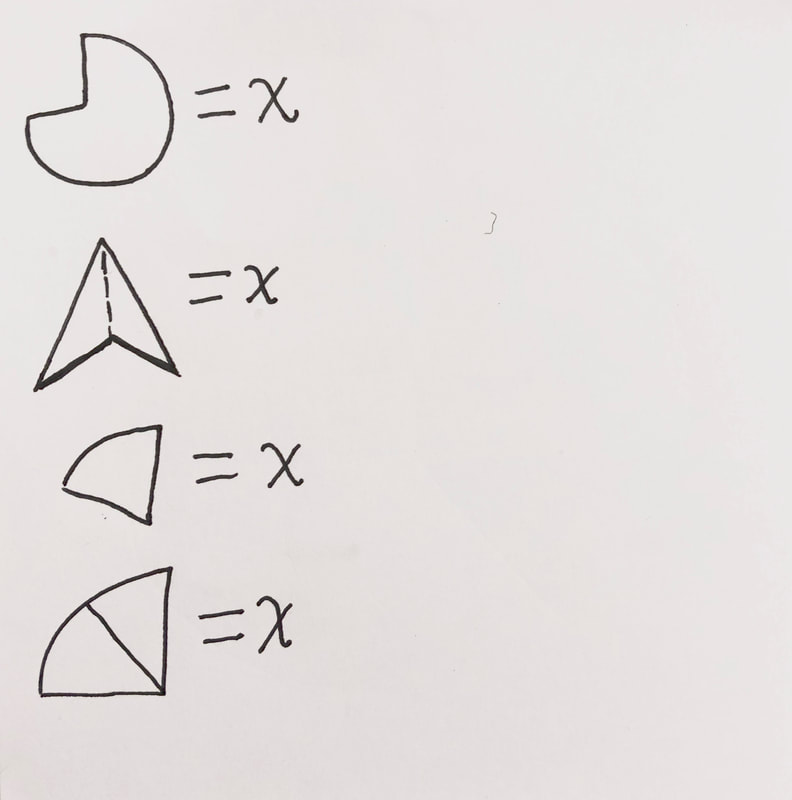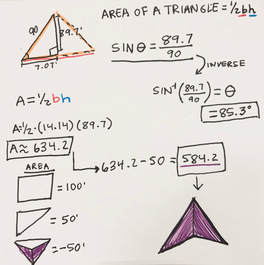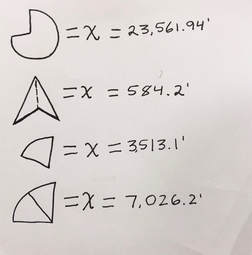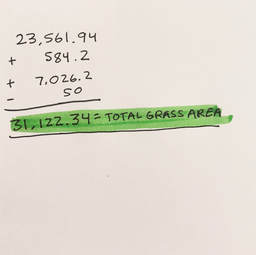Problem Statement
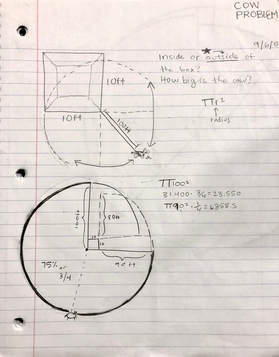
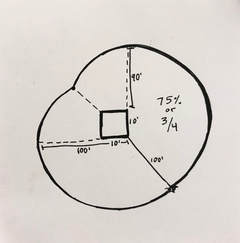
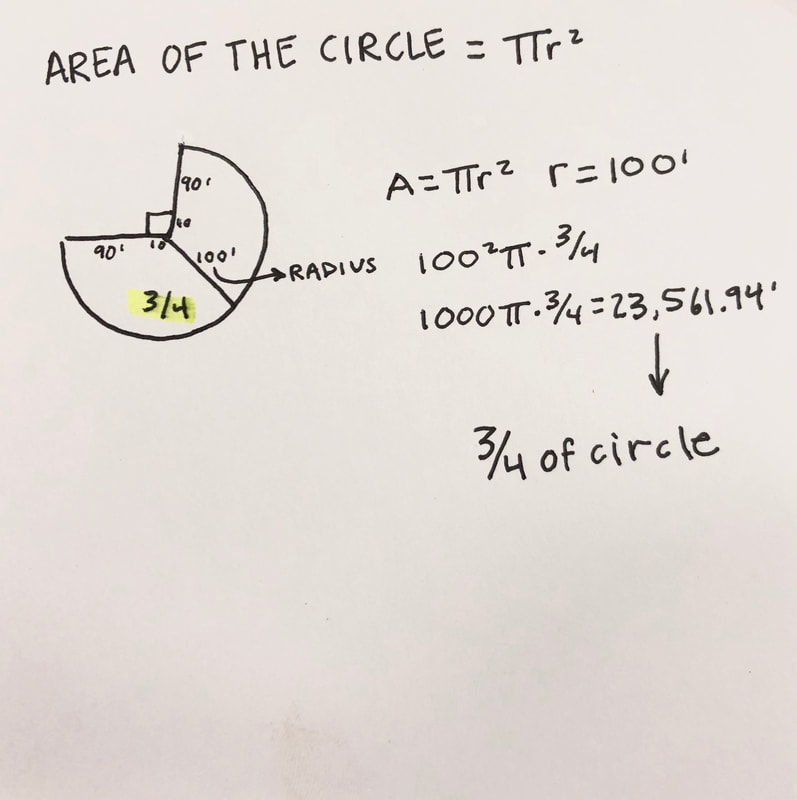
There is a barn with the measurmentd 10'x10', there was a cow attached on a side of the barn with a rope with the length of 100'.
The question was, 'How much the area of the land the cow can graze."
The question was, 'How much the area of the land the cow can graze."
Process
In groups, we were introduced to this problem with very minimal information, the barn, and the rope's measurments.
Individually we had to write down all our initial ideas, then share out. At first I just thought about drawing a box, the rope, then a circle which would be where the cow can graze. I thought the circle would be a complete circle that would be 100ft all around.
After having the diagram finished and knowing what we needed the find, we found that breaking the diagram in actual smaller more specific shapes that we actually know how to solve for, like a triangle. After breaking it up we can add everything together to get the total area, which will make it a lot easier.
The dimensions required to solve this problem:
-The height of the line through the triangle. -The base of the triangle, the line cutting the barn in half. |
Solution
1. Find the area of the circle
Here I started by getting familiar with the formula to solve for the are of a circle.
A = π r^2 Then I identified what we needed to plug in : r = radius Then I multiplied that by 3/4 because we want to find only that amount of the circle. Then I just solved the equation. A = 100^2 π x 3/4 A = 1000 π x 3/4 Area of 3/4 of the circle = 23,561.94 |
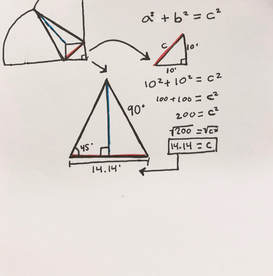
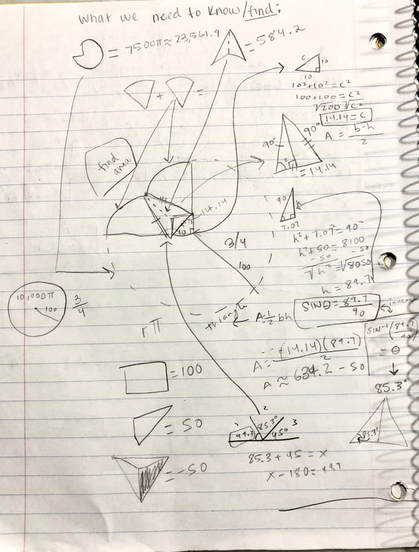
2. Using the Pythagorean Theorem to find base of triangle
|
a^2 + b^2 = c^2
I started by identifying 1/2 of the barn and the measurements we already have to plug into the Pythagorean Theorem. 10^2 + 10^2 = c^2 Then just solved the equation to find "c"= The base of the triangle. 10^2 + 10^2 = c^2 100 + 100 = c^2 200 = c^2 √200 = √c^2 14.14 = c (Base of triangle) |
3. Using the Pythagorean Theorem to find height of triangle
|
a^2 + b^2 = c^2
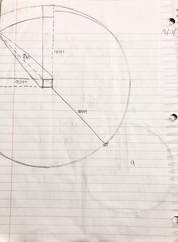
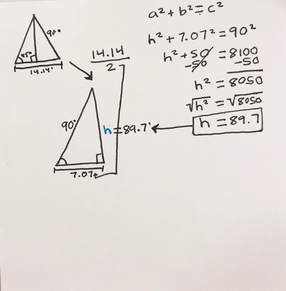
I then cut that triangle into a right triangle which will make it easier to solve. This involved dividing the base by 2. 14.14 / 2 = 7.07 Then I just again identified what I needed to plus into the equation. h^2 + 7.07^2 = 90^2 h^2 + 50 = 8100 -50 -50 h^2 = 8050 √h^2 = √8050 Height of triangle = 89.7 |
|
4. Area of triangle - barn
|
A = 1/2 b x h
I plugged in everything we needed into the formula to find the area of the triangle, which is what we just solved for. The base = 14.14 & the height = 89.7 . A = 1/2 (14.14) (89.7) Area of triangle = 634.2 Now the cow cannot graze into the barn so I took the total area of the barn which was 100 (10x10) and divided that in 2 to get half of the barn included in the triangle. Then I subtracted 50 from the total area of the triangle (634.2). 634.2 - 50 = 584.2 |
5. Using SOH-CAH-TOA to find the angle to solve for the sectors
|
Now after finding the height and base we have everything required to plug into the next equation using: SOH-CAH-TOA
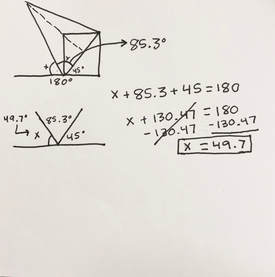
SIN θ = 89.7 / 90 Since we have the opposite = 89.7 & the hypotenuse = 90, we can plug it into the inverse formula. SIN^-1 (89.7 / 90) = θ 85.3 = θ (Angle of triangle) Then we know they all (85.3, 45, and x) add up to 180, so we just put it into a formula and solve for x, our missing angle. x + 85.3 + 45 = 180 x + 130.47 = 180 -130.47 -130.47 x (missing angle from sector) = 49.7 |
|
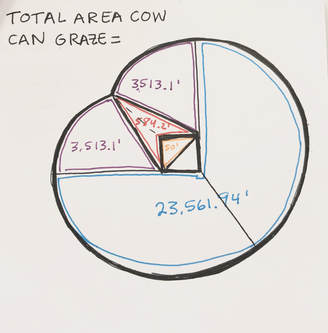
5. Finding the: (area of the circle + area of triangle + area of sector - 1/2 of barn) = Total area the cow can graze
|
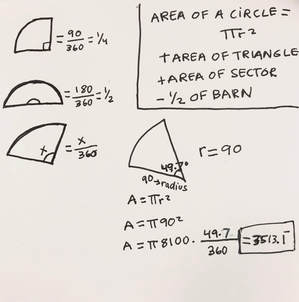
First I overlooked the problem by giving examples of 1/4 of a triangle, 1/2 of a triangle, and the unknown of a triangle, which is what we are trying to find.
The numerator is the angle of the slice (49.7 is angle of the sector). Everything will be divided by 360 because thats the degree of the full circle. x / 360 Again using the formula: A = π r^2 + x / 360 = Area of sector A = π 90^2 x 49.7 / 360 Area of sector = 3,513.1 |
|
6. Adding everything together
Now that we have all our information and measurement we can solve using the formula we created for our solution at the very beginning.
(Area of 3/4 of circle)+(Area of Triangle)+2(Area of sector)-(Area of 1/2 of the barn) = Total Area Cow Can Graze
|
23,561.94 + 584.2 + 2(3,513.1) - 50 = Total Area Cow Can Graze
|
Evaluation/Reflection
|
What pushed my thinking was probably being asked by many of my peers and friends on how to do the problem. This not only let me help them, but it really helped me understand it more. Even as I am writing this I helped someone today and it pushed my thinking even though I had already solved the problem.
Out of the whole problem I got to understand SOH-CAH-TOA a lot better. I was taught this in freshman year but, I never really actually understood the concept of it. It was just about memorizing the steps. Now I got a refresher and feel a lot more confident in using this method. I actually tend to gravitate more towards that for some reason, which I thought I would never. The group quiz was a positive impact in me because in my group was 4 people that had 4 different ways of learning. Sometimes that overwhelms me, but sometimes I really like it because I can see all the different ways people look at problems. I also liked doing the quiz with a group because we ended up going very slow with each step, which made me rethink the problem many times before skipping and going to the next step. If I were to grade myself in this unit I think I would give myself an A+ because I have been becoming more of a leader and I feel like teaching this problem that is very complicated gave me confidence in myself and gave me a much better understanding in all the concepts we learned in. So knowing that tackling this hard problem a lot more "publicly" making mistakes will be pretty easy, and I was okay with that because it actually gave me a chance to learn. |
|
