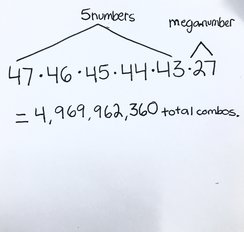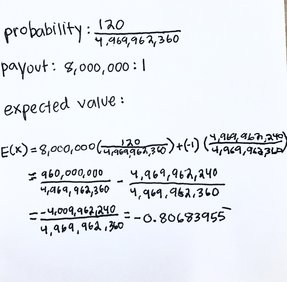Problem Statement
|
At the beginning of the semester, we guessed the odds of winning the CA Super Lotto (my guess was 1 in a million chance).
The rules are simple: 1. Choose any 5 numbers between 1-47 (these numbers will not be repeated) 2. Pick a mega number between 1-27 (this number may repeat) 3. Match all 5 numbers and the mega number and you win! We then played it and used a number generator, and realized the odds of winning are very low. This leaded on to our 3 questions:
1.) How many different number combinations are possible for a CA Super Lotto ticket? 2.) What is the propability of winnning the CA Super Lotto? 3.) If you match all 6 numbers, you win $8,000,000. It costs $1 to play. WHat are your expected winnings? |
Process & Solution
The very first day we were given the chance to play the CA Super Lotto. We first chose our 6 numbers:
Nobody won... We then questioned the chances of winning, I guessed 1 in a million. This was the launch of our project!
How many different number combinations are possible for a CA Super Lotto ticket?
|
You have to choose 5 numbers between 1-47 (does not repeat), and pick a mega number between 1-27 (may repeat). So instead of multiplying 47^5, it would be 47*46*45*44*43 because every time, you are removing a number from the total=47 to be one out of the 5 numbers your pick. Then the total would be 46, and from this remove another number...etc. I also multiplied 27 because the number can be repeated when chosen.
|
What is the probability of winning the CA Super Lotto?
|
To win you have to match all 5 numbers and the mega number. The denominators is the sample space, which we have done in the first questions, the numerator is how many numbers are left. So there it is 5/47 because 5 numbers need to be picked from the total amounts of numbers=47. Then it is 4/46 because 1 number has been picked so instead of 5 numbers now it would be 4 numbers you need to pick...etc. It is 1/27 because it is only 1 mega number from the total=27. Then once I multiplied all those I got 120/4,969,962,360 which can be simplified down.
|
If you match all 6 number, you win $8,000,000. It costs $1 to play. What are your expected winnings?
|
To find the expected winnings I used the expected value formula and plugged all the information I had in. So( $8,000,000) is how much you will get if you win * the probability of winning, which was (120 / 4,969,962,360), then you add the probability of losing which is (-1) (4,969,962,240 / 4,969,962,360). Then once you solve it and round the decimal, you lose .81 cents with each Lotto ticket you buy.
|
Expected Value- E(X)=∑ xi pi
Problem Evaluation
I liked this problem because you can use these skills in the real world and because we did activities that actually made me understand the whole topic a lot better. It was challenging but in the good kind of way. Sometimes I found myself understanding something really well once I really thought about it and discussing why I thought it; and sometimes I was struggling and not understanding a single thing, even though some people in my table tried explaining it many times. I always tried very hard to try to understand what the problem was saying and how to solve it because I like helping people because Ive been in the shoes of someone who might have a difficult time to understand something and struggles. And I think since I've been in that situation in the past math years, I can explain it in a way understanding how they are feeling, if that kind of make sense. So I think that was something that pushed my thinking. I learned that making mistakes are good because you can learn from them, and including yourself in the conversation helps a lot.
Self Evaluation
If I were to grade myself on this probability unit, I would give myself an A because I feel like I really stepped up in effort and confidence to make mistakes, I feel like I really contributed to the group with my work weather I was right or wrong. Plus I always would put my voice in the conversations. I am really proud of myself because I felt like before with the people that are in my group I wouldn be able to do what I did because of how "smart" they were. Not only I speaked up I felt like one of the leaders.
Edits
Edits from my peers:
-Fix grammer
-Adjust layout
-Expand in Self Evaluation
-Fix grammer
-Adjust layout
-Expand in Self Evaluation