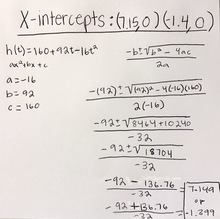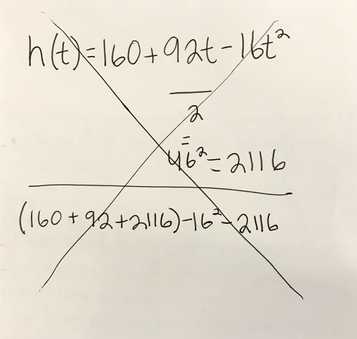Fireworks Problem

Problem Statement

"The Jefferson High JV soccer team has won the championship. To celebrate this triumph, the school will be putting on a firework display. The fireworks will be launched from the top of a school tower. The director isn't concered about the cost, but he wants your help with the timing mechasnism that denotates the fireworks, and he's also worried about the saftey of the spectators."

We were given the following information:
-65 degree launch angle from the horizontal
-The initial velocity: 92 ft./sec.
-The height of the tower: 160 ft.

For this problem we are solving for the vertex and the x-intercepts:
-Unknown peak of the fireworks
-Unknown distance it will travel

Equations Given:
h(t)=160+92t-16t^2 and d(t)=92t/tan65

Process & Solution

We made direct/specific questions about what and how we needed to solve for.
Ex: What do the x-intercepts represent & how can we find them?
What is the highest peak?
How can we solve for the vertex?

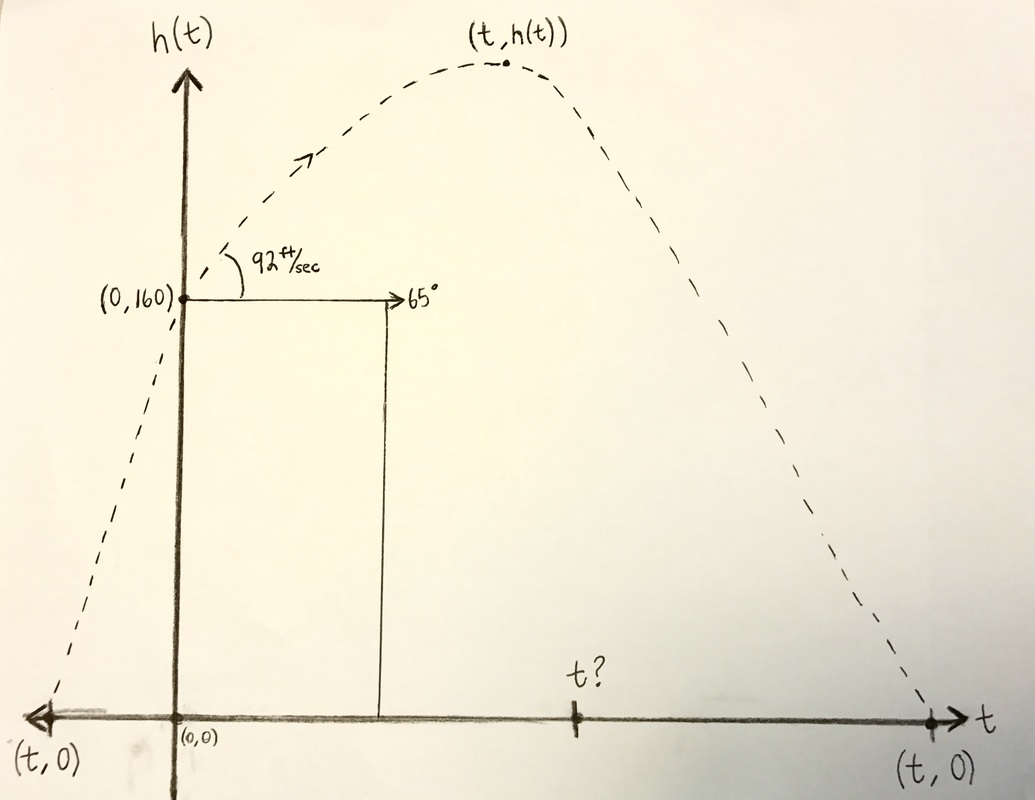
We created a diagram including all the information we were given.

I used the quadratic formula to find the x-intercepts. Aka: Distance it will travel

I solved for the vertex. For the middle x point = t I added both x intercepts then divided the sum by 2. I then subtracted 1.44 from the sum because the start of the launch was at (0,0) not (-1.44,0) Then I plugged t which was what we just solved for into the standard formula which gave us h(t). Aka: Peak of fireworks

I plugged the x intercept into t in this formula.

Here is all the solved information :)

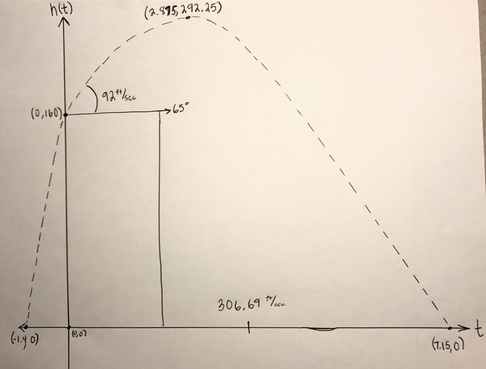
When I first attempted this problem I found it quite easy. All I had to do was find the x-intercepts, and the vertex. So first I started with the x-intercepts, I used the quadratic formula because I really like using that equation. Then finding the distance in time was simple to me too because all I had to do was plug in the x intercept into the equation and solve it.

At first for the vertex, I thought about using the equation h(t)=160+92t-16t^2 and dividing it by 2 and squaring it. But then I ran into a bump and asked why it wasn't working. Then we realized that there was something different about the equation. That it had a number for a=16 instead of just being x an unknown number. So what we had to do instead was get the middle point of 0 to the positive x intercept. Because the launch happens on point 0 not a negative point; this gives us the x intercept. Then we plugged in that sum into the equation for t ; which then gave us the y intecept.

Final Graph

Problem Evalutation

We were first given this problem in the begining of the year not knowing what parabolas were, or how to solve for the vertex and the x intercpets. Now at the ending of this unit/semester we were re-given the problem to solve with the knowledge we now have. I didn't love the problem but I didn't hate it. I feel like the old me would hate it... I say this because this semster was differnent. I actually started asking questions and was comfortable getting things wrong and starting over again. And because of that I was learning easier and much faster and I felt like I really understood what I was doing throughout this problem. I do admit it felt pretty good getting the answers right, this was something that pushed me because I know although I might be struggling I will always have that feeling and relief when I finish. I got the most out of the quadratic formula because I memorized the formula and knew what to use it for and what to plug in eaisly.

Self Evaluation

If I were to grade myself in this quadratics unit I would give myself an A because throughout the whole unit I felt as if I really understood what I had to do and if I didn't I would push myself to think harder and ask for help. And that has been a struggle of mine since the very first math class I have ever had, And I would always be afraid to go to the class because I new I wouldn't understand. But this year, most of the time I found myself helping my tablemates understand what we were doing and I feel as if that helped me a lot more in my understanding because you need to know how to explain and teach something to someone in order to really understand the problem. And if I didn't know how to solve something my tablemates would all help eachother out equally by setting down questions, or by asking others by using different methods and stratagies.