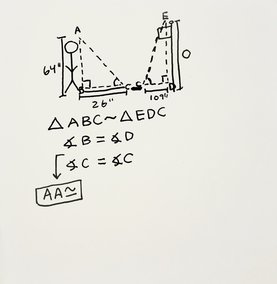Problem Statement
We were asked to find the height of the flagpole so we could get a new flag. We had to figure the length of the pole without actually having to measuring it.
Process & Solution
We first got introduced to this problem with a handout that we answered in class. It had questions like what is our initial guess for the height of the flagpole (min. & max. ft), my guess was a minimum of 23ft and a maximum of 30ft. We then went outisde to take some observations of the flagpole to get a more accurate prediction of the height, we noticed that we can "compare" our height to find it unknown height of the flagpole.
We then were introduced to similarity, which basically is: the same shape but different size. Shapes or polygons to be similar have to have corresponding sides with an equal angle. I learned it's always easier to disprove something than to prove that it is similar because once there is something that's different it can no longer be similar. While finding something that is the same, like having a shapes corresponding angles equal doesn't mean they are similar since they can have different corresponding lengths.
We then were introduced to similarity, which basically is: the same shape but different size. Shapes or polygons to be similar have to have corresponding sides with an equal angle. I learned it's always easier to disprove something than to prove that it is similar because once there is something that's different it can no longer be similar. While finding something that is the same, like having a shapes corresponding angles equal doesn't mean they are similar since they can have different corresponding lengths.
Shadow Method
Estimated flagpole height : 24'
|
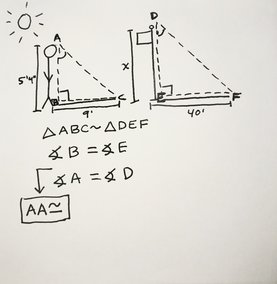
We first drew a visual representation/diagram of person and persons shadow, the flagpole and the flagpoles shadow. We then added the proportions/measurements to our diagram that were necessary to calculate the height (5'4"= persons height, 9'=persons shadow, x=flagpole height, 40'=flagpole shadow). Then using the shadow method formula we plugged in the numbers and solved for x by cross multiplying (5'4"/9' = x/40'). Then we got our estimated flagpole height (24=x).
|
We can form 2 similar triangles with the shadow method because we justified it with AA theorem (angle angle). ∢B ≅∢E & ∢A≅∢D AA~
The first angles, both person and flagpole have a 90° angle, The second angles, both person and flagpole share the suns fixed angle. With this much information it is enough to prove that the two triangles are similar. AA theorem: 2 corresponding angles are equal |
Mirror Method
Estimated flagpole height : 22.36'
|
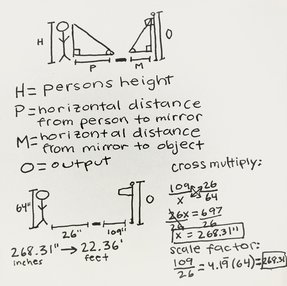
We first assigned variables for measurements we needed to find the height of the flagpole, then drew a visual representation/ diagram of person and person to mirror, flagpole, flagpole to mirror (H=64", P=26", M=109", O=output/flagpoles height). Then using the mirror method formula we plugged in the numbers and solved for O by cross multiplying or using scale factor (CM 109"/O = 26"/64" -- SF 109"/26"= O(64")).Then we got our estimated flagpole height (268.31" or 22.36').
|
We can form 2 similar triangles with the shadow method because we justified it with AA theorem (angle angle). ∢B ≅∢D &∢ A≅∢E AA~
The first angles, both person and flagpole have a 90° angle, The second angles, both person and flagpole share the mirrors reflection fixed angle. With this much information it is enough to prove that the two triangles are similar. AA theorem: 2 corresponding angles are equal |
Clinometer Method
Estimated flagpole height : 32.6'
|
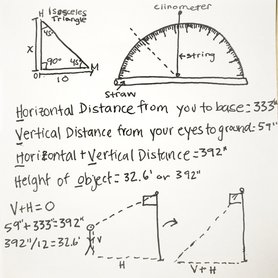
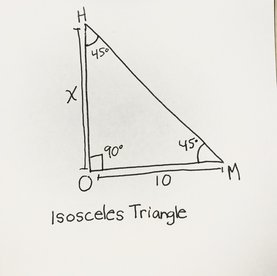
We first drew and labeled a diagram representing a right angled isosceles triangle. Then using the clinometer we measured everything we needed to find the height(H=333", V=59", H+V=O= Height of flagpole). A clinometer has a straw on the on thetop and a string attached that when the tool is tilted to look through the straw and see the object it measures and gives you the angle you are creating to see the object. This tool measures the angle of elevation, or angle from the ground, in a right - angled triagnle. Then using the clinometer method formula we added the H(horizontal distance) and V(vertical distance) because when using the cinometer your looking to find the angle from your eyes because that's the only way you can measure it, but you are standing up so there is still that distance from your eyes to the floor you need to add to create a whole length as if you were laying on the floor (H+V=392"). Then for the total height of the flagpole, O. We converted the length into feet and got our estimated flagpole height (O= 392"/12 = 32.6').
|
Isosceles Triangle:
A triangle that has two sides of equal length and two equal angles. |
Final Estimation
My final estimation of the height of the flagpole is 25' because it seems the most accurate since the shadow and mirror method (S=24', M=22') are the closest together and the clinometer seem to have the most off measurments. I feel like you can get an accurate measurment with this method but you have to be very presice and have to have the perfect angle (exactly 45°) to get the actual height which I think a lot of us just measured quickly. So 25' is my final esitmate.
Problem Evaluation
I liked this problem because it was very hands on and I used tools that I've never used. I also feel that we can actually used what we learned in the future with these methods and tools. I really liked the section of finding similarity and the problems we were solving here because I felt like I really understood them and if I was stuck on it in the beginning I really tried to figure it out since I have been understanding everything else, it would just push my thinking.
Self Evaluation
If I were to grade myslelf on this similarity unit I would recive an A+ because I feel like since I could solve the problems I would be able to help my group if they were stuck and I know you haven't mastered a topic till you can teach it so helping them helped me. I contributed within group conversations and we always tried to communticate throughout solving our problems so we were all on track.
Edits
- Bold titles
- More in dept in Self & Problem Evaluation
- Fix grammar