Problem Statment
A rectangle has one corner on the graph of y=16-x^2, another at the orgin, a third onthe positive y-axis, and the fourth on the positive x-axis. If the area of the rectangle is a function of x, what value of x yields the largest area for the rectangle.
Process
|
When we were presented this problem the very first thing we had to do was write down questions we had about the question given. Things we didn't understand or wanted clarification on. After that we shared and answered them as a group.
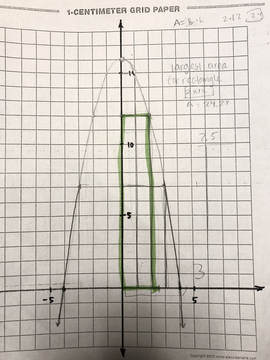
My initial attempt was to try and factor the equation, for some reason. When we shared with our group our process a lot of us had empty pages and we weren't really sure what we were doing. After a while of brainstorming and factoring correctly, Mr. Carter helped us out by pointing at a graph and what we could do with it. Plot the points! We started with the basic y and x intercepts, and made our parabola, then we sketched out a few rectangles inside the parabola. To find the largest area I initially found it the easiest way was just to count the squares inside the box. But it wouldn't give me the area. I knew which one it would be though. So we then plugged it into the equation. After plugging it in, we were a little stuck because we thought that was the final estimated area. We then realized that there could be super tiny points like 1.1, 1.2, 1.3, that could have the largest area instead of the whole number. So we created a x and y table. We stopped calculating them when the number began the become lower, so then we found the closest answer. The function we used to find this was, A=16x-x^3. Our initial attempts to finding the perimeter was just plugging in the equating for perimeter: P=2(x+y). Then we simplified the function to, P=-2x^2+2x+32. We then found the max vertex which gave us the max perimeter. We new these functions were correct because it was giving us the correct answers when plotting them on the graph. |
Solution
We ended up having the maximum perimeter = to be 32.5. We found this by solving the formula P=-2x^2+2x+32, and plugging in x, which we found by making the x and y table and finding the max x intercept be= 0.5, and the y to be 15.75 which was the vertex and the side lengths of the rectangle.
The max area our group concluded with was 24.63. Our groups initial guess was 24. We found this by plugging in the x intercepts into the formula to get the y. Once we had the biggest whole number, 24. We new there was a bigger number if we got into the hundreds, which we then did and got the final answer to be a=24.63 (2.3, 10.71).
The max area our group concluded with was 24.63. Our groups initial guess was 24. We found this by plugging in the x intercepts into the formula to get the y. Once we had the biggest whole number, 24. We new there was a bigger number if we got into the hundreds, which we then did and got the final answer to be a=24.63 (2.3, 10.71).
Group Test/ Individual Test
A day before our tests we prepared as a group by using the same problem but just changing the numbers in the function. y=__-x^2
At first when preparing we were very lost, we completely forgot about the whole process and how we found the solution. Little by little we started finding clues in our journals of how we found the maximum perimeter and area and it made sense by the end of the period. But, it took a while, don't get me wrong. It looked like we were all pretty much understanding it or remembering.
When we took the quiz as a group, it was a little unexpected. Everything was so confusing, we knew what was suppose to be done but there were little mistakes we came across that caused us to keep pausing. I think our group was just thinking about it way to much and we were very indecisive. By we, I mean me. I was so lost because I knew how to do it, but it was weird not being able to do it as a whole. The good thing was, we all communicated very well in what we were. doing to each other or what we didn't understand. We really weren't afraid to share our ideas.
It was so weird because when it came to the individual test, it was so easy. I probably did it all in 3 minutes. It was like engraved in my brain which was pretty cool because I knew what I was doing.
I usually like group tests, I think it was just the over thinking that got me while the test. Overall I liked it, including both individual and group.
At first when preparing we were very lost, we completely forgot about the whole process and how we found the solution. Little by little we started finding clues in our journals of how we found the maximum perimeter and area and it made sense by the end of the period. But, it took a while, don't get me wrong. It looked like we were all pretty much understanding it or remembering.
When we took the quiz as a group, it was a little unexpected. Everything was so confusing, we knew what was suppose to be done but there were little mistakes we came across that caused us to keep pausing. I think our group was just thinking about it way to much and we were very indecisive. By we, I mean me. I was so lost because I knew how to do it, but it was weird not being able to do it as a whole. The good thing was, we all communicated very well in what we were. doing to each other or what we didn't understand. We really weren't afraid to share our ideas.
It was so weird because when it came to the individual test, it was so easy. I probably did it all in 3 minutes. It was like engraved in my brain which was pretty cool because I knew what I was doing.
I usually like group tests, I think it was just the over thinking that got me while the test. Overall I liked it, including both individual and group.
Evaluation/ Reflection
I think what really pushed my thinking was my group as a whole, was how all of our levels of understanding of certain topics were different. So we had to and were constantly working together because some of my peers knew how to do things I didn't, and I knew how to do things that they didn't. The most I got out of it is being open to different ideas and listening to peoples ideas because if you over think things it won't turn out good. I think I would grade myself and A because I feel like in class I always tried although this unit or question was a bit more challenging for me. I asked many questions without fear of being wrong. And my group as a whole were very good listeners and good at explaining to each other about steps we wouldn't understand.